本文共 2054 字,大约阅读时间需要 6 分钟。
1.JVM 基本机构
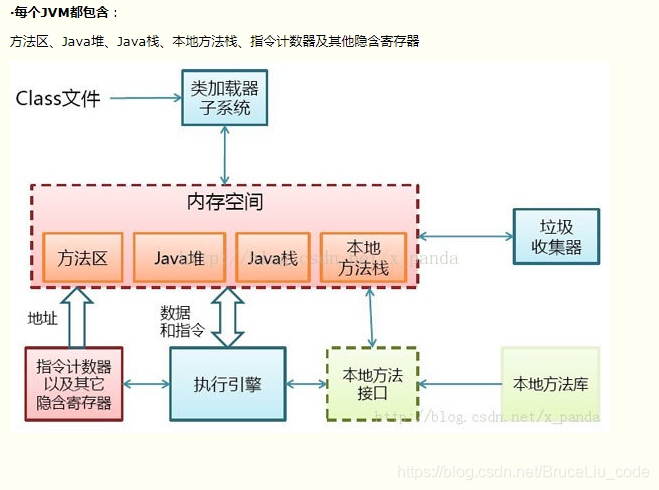
1.1 类加载子系统负责从文件系统或者网络中加载Class信息,加载的类信息存放于一块称为方法区的内存空间。除了类的信息外,方法区中可能还会存放运行时常量池信息,包括字符串字面量和数字常量(这部分常量信息是Class文件中常量池部分的内存映射)。
1.2 java堆在虚拟机启动的时候建立,它是java程序最主要的内存工作区域。几乎所有的java对象实例都存放在java堆中。堆空间是所有线程共享的,这是一块与java应用密切相关的内存空间。
1.3 每一个java虚拟机线程都有一个私有的java栈,一个线程的java栈在线程创建的时候被创建,java栈中保存着帧信息,java栈中保存着局部变量、方法参数,同时和java方法的调用、返回密切相关。
1.4 本地方法栈和java栈非常类似,最大的不同在于java栈用于方法的调用,而本地方法栈则用于本地方法的调用,作为对java虚拟机的重要扩展,java虚拟机允许java直接调用本地方法(通常使用C编写)
1.5 垃圾回收系统是java虚拟机的重要组成部分,垃圾回收器可以对方法区、java堆进行回收。其中,java堆是垃圾收集器的工作重点。和C/C++不同,java中所有的对象空间释放都是隐式的,也就是说,java中没有类似free()或者delete()这样的函数释放指定的内存区域。对于不再使用的垃圾对象,垃圾回收系统会在后台默默工作,默默查找、标识并释放垃圾对象,完成包括java堆、方法区和直接内存中的全自动化管理。
1.6 PC(Program Counter)寄存器也是每一个线程私有的空间,java虚拟机会为每一个java线程创建PC寄存器。在任意时刻,一个java线程总是在执行一个方法,这个正在被执行的方法称为当前方法。如果当前方法不是本地方法,PC寄存器就会指向当前正在被执行的指令。如果当前方法是本地方法,那么PC寄存器的值就是undefined
1.7 执行引擎是java虚拟机的最核心组件之一,它负责执行虚拟机的字节码,现代虚拟机为了提高执行效率,会使用即时编译技术将方法编译成机器码后再执行。
2.Java 代码编译和执行的整个过程
2.1 Java 代码的编译是由 Java 源码编译器来完成,流程图如下所示:
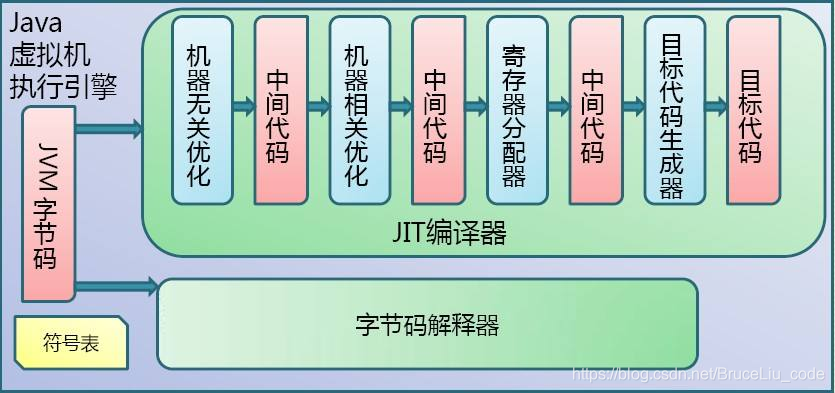
2.2 Java字节码的执行是由JVM执行引擎来完成,流程图:
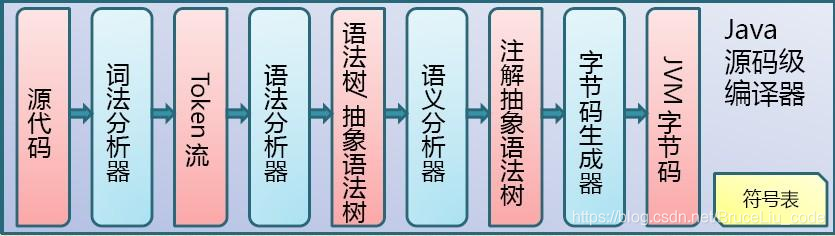
2.3 Java代码编译和执行的整个过程包含了以下三个重要的机制:
1.Java源码编译机制
Java 源码编译由以下三个过程组成:1.分析和输入到符号表2.注解处理3.语义分析和生成class文件
最后生成的class文件由以下部分组成:
1.结构信息。包括class文件格式版本号及各部分的数量与大小的信息2.元数据。对应于Java源码中声明与常量的信息。包含类/继承的超类/实现的接口的声明信息、域与方法声明信息和常量池3.方法信息。对应Java源码中语句和表达式对应的信息。包含字节码、异常处理器表、求值栈与局部变量区大小、求值栈的类型记录、调试符号信息
2.类加载机制
JVM的类加载是通过ClassLoader及其子类来完成的,类的层次关系和加载顺序可以由下图来描述: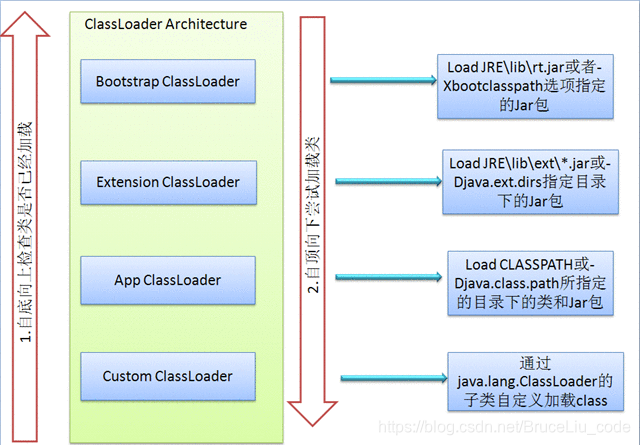 1.Bootstrap ClassLoader /启动类加载器,$JAVA_HOME中jre/lib/rt.jar里所有的class,由C++实现,不是ClassLoader子类
1.Bootstrap ClassLoader /启动类加载器,$JAVA_HOME中jre/lib/rt.jar里所有的class,由C++实现,不是ClassLoader子类 2.Extension ClassLoader/扩展类加载器,负责加载java平台中扩展功能的一些jar包,包括$JAVA_HOME中jre/lib/*.jar或-Djava.ext.dirs指定目录下的jar包
3.App ClassLoader/ 系统类加载器,负责记载classpath中指定的jar包及目录中class
4.Custom ClassLoader/用户自定义类加载器(java.lang.ClassLoader的子类),属于应用程序根据自身需要自定义的ClassLoader,如tomcat、jboss都会根据j2ee规范自行实ClassLoader加载过程中会先检查类是否被已加载,检查顺序是自底向上,从Custom ClassLoader到BootStrap ClassLoader逐层检查,只要某个classloader已加载就视为已加载此类,保证此类只所有ClassLoader加载一次。而加载的顺序是自顶向下,也就是由上层来逐层尝试加载此类。
3.类执行机制
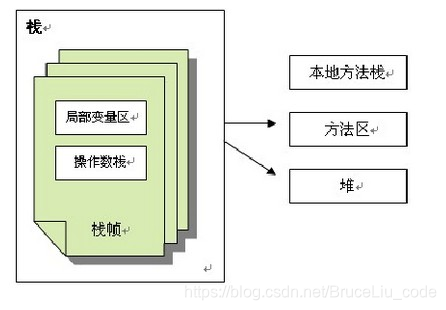
JVM是基于栈的体系结构来执行class字节码的。线程创建后,都会产生程序计数器(PC)和栈(Stack),程序计数器存放下一条要执行的指令在方法内的偏移量,栈中存放一个个栈帧,每个栈帧对应着每个方法的每次调用,而栈帧又是有局部变量区和操作数栈两部分组成,局部变量区用于存放方法中的局部变量和参数,操作数栈中用于存放方法执行过程中产生的中间结果。栈的结构如下图所示:
转载地址:http://nddu.baihongyu.com/